Di–stri–bu-tivgesetz → "Die Striche bündeln"
Auf dieser Seite:
Distributivgesetz für Multiplikation und Addition
Erklärung
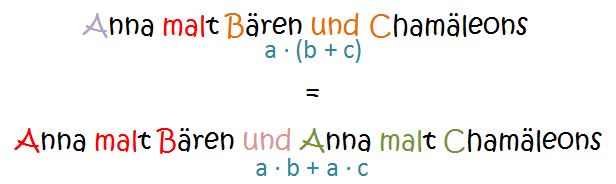
Anna malt Bären und Chamäleons.
Die Bilder, die dabei herauskommen sind zwar eher durchschnittlich, aber dieser einfache Satz hat es trotzdem in sich!
Analysieren wir mal:
Der Satz enthält 2 Aussagen:
- Anna malt Bären
- Anna malt Chamäleons
Diese bahnbrechende Erkenntnis ermöglicht es uns nun, den Satz auch anders schreiben. Die Bedeutung ändert sich dadurch nicht:
Anna malt Bären und Anna malt Chamäleons.
Was bringt das nun? Was hat das mit diesem Distributivgesetz zu tun?
Beim Distributivgesetz passiert genau das gleiche! Wir müssen nur ersetzen:
- Anna → a
- Bären → b
- Chamäleons → c
- malt → ⋅
- und → +
Wegen der Regel „Punkt- vor Strichrechnung“ müssen wir bei der mathematischen Schreibweise Klammern setzen:
Genau das besagt das Distributivgesetz:
Regel
Soll eine Summe mit einer Zahl multipliziert werden, kann man auch die einzelnen Summanden mit der Zahl multiplizieren und erst dann addieren. Das Ergebnis ändert sich dadurch nicht!
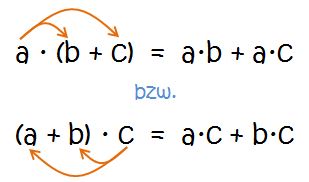
Beispiele
Überprüfen wir das an Hand von ein paar Beispielen:
5 ⋅ (3 + 4) = 5 ⋅ 7 = 35
5 ⋅ 3 + 5 ⋅ 4 = 15 + 20 = 35
16 ⋅ (23 + 17) = 16 ⋅ 40 = 640
16 ⋅ 23 + 16 ⋅ 17 = 368 + 272 = 640
(10 + 8) ⋅ 6 = 18 ⋅ 6 = 108
10 ⋅ 6 + 8 ⋅ 6 = 60 + 48 = 108
mehrere Summanden
Es funktioniert auch mit längeren Ausdrücken:
Anna malt Bären und Anna malt Chamäleons und Anna malt Dachse und Anna malt Elefanten.
ist das gleiche wie
Anna malt: Bären und Chamäleons und Dachse und Elefanten.
Wir ersetzen genauso wie oben und außerdem:
- Dachse → d
- Elefanten → e
Und erhalten somit
a ⋅ b + a ⋅ c + a ⋅ d + a ⋅ e = a ⋅ (b + c + d + e)
Wofür braucht man das Distributivgesetz
Durch Anwendung des Distributivgesetz ergeben sich manchmal Rechenvorteile!
Je nach Aufgabenstellung ist das Distributivgesetz in die eine oder in die andere Richtung anzuwenden.
Beispiel: Rechne 4 ⋅ 23 im Kopf. Vermutlich gehst Du dabei so vor:
4 ⋅ 23 =
4 ⋅ (20 + 3)=
4 ⋅ 20 + 4 ⋅ 3
80 + 12=
92
Manchmal bringt auch die Umgekehrung einen Rechenvorteil: 6 ⋅ 43 + 6 ⋅ 57
6 ⋅ 43 + 6 ⋅ 57 =
6 ⋅ (43 + 57)=
6 ⋅ 100=
600
11 ⋅ 3 ⋅ 2 + 11 ⋅ 1 + 11 ⋅ 3 =
11 ⋅ (3 ⋅ 2 + 1 + 3)=
11 ⋅ (6 + 1 + 3)=
11 ⋅ 10=
110
Distributivgesetz Eselsbrücke
Die Deutsche Bezeichnung für das Distributivgesetz lautet Verteilungsgesetz.
Über den Begriff Verteilungsgesetz kann man ganz gut auf die Regel kommen, denn die Zahl mit der die Summe multipliziert wird, wird auf die einzelnen Summanden „verteilt„.
Doch wie kann man sich den Begriff Distributivgesetz merken?
Wenn Du Latein kannst, ist es einfach: distribuere (lat.) bedeutet verteilen. Vielleicht kennst Du auch das englische Wort to distribute mit der gleichen Bedeutung.
Oder, Du merkst Dir die Eselsbrücke:
Di–stri–bu-tivgesetz → "Die Striche bündeln"
(Die Strichrechnungen werden in einer Klammer „gebündelt“)
Distributivgesetz – Varianten
Distributivgesetz für Multiplikation und Subtraktion
Soll eine Differenz mit einer Zahl multipliziert werden, kann man auch erst den Minuenden und den Subtrahenten mit der Zahl multiplizieren und erst dann subtrahieren. Das Ergebnis ändert sich dadurch nicht!
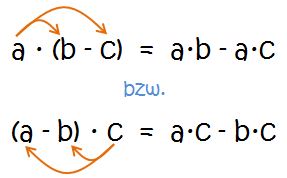
Beispiele:
4 ⋅ (6 – 2) = 4 ⋅ 4 = 16
4 ⋅ 6 – 4 ⋅ 2 = 24 – 8 = 16
15 ⋅ (28 – 12) = 15 ⋅ 16 = 240
15 ⋅ 28 – 15 ⋅ 12 = 420 – 180 = 240
Distributivgesetz für Division und Addition (bzw. Subtraktion)
Soll eine Summe (bzw. Differenz) durch eine Zahl dividiert werden, kann man auch die einzelnen Summanden (bzw. Minuend und Subtrahent) durch die Zahl dividieren und erst dann addieren (bzw. subtrahieren). Das Ergebnis ändert sich dadurch nicht!
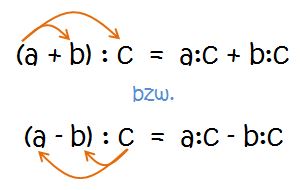
rechtsdistributiv und linksdistributiv
Im Gegensatz zu den vorherigen Regeln gilt diese Regel nur, wenn die Summe (bzw. Differenz) durch eine Zahl dividiert wird. (→ rechtsdistributiv)
Es funktioniert nicht, wenn eine Zahl durch eine Summe (bzw. Differenz) dividiert werden soll. (→ nicht linksdistributiv!)
Beispiele:
(15 + 18) : 3 = 33 : 3 = 11
15 : 3 + 18 : 3 = 5 + 6 = 11
(24 – 6) : 2 = 18 : 2 = 9
24 : 2 – 6 : 2 = 12 – 3 = 9
Es geht aber nicht:
24 : (4 + 2) = 24 : 6 = 4
24 : 4 + 24 : 2 = 6 + 12 = 18
36 : (18 – 12) = 36 : 6 = 6
36 : 18 – 36 : 12 = 2 – 3 = nicht 18…
Ausklammern
Ist eine Summe von Produkten gegeben, dann kann man gemeinsame Faktoren ausklammern
[Bild: a x (b+c+d+e) = ab + ac + ad + ae]
Beispiele:
3 ⋅ 2 + 3 ⋅ 5 + 3 ⋅ 7 + 3 ⋅ 3 = 6 + 15 + 21 + 9 = 51
3 ⋅ (2 + 5 + 7 + 3) = 3 ⋅ 17 = 51
Ausmultiplizieren
Soll eine Summe mit einer Zahl multipliziert werden, kann man auch die einzelnen Summanden mit der Zahl multiplizieren und erst dann addieren.
[Bild: a x (b+c+d+e) = ab + ac + ad + ae]
Beispiele:
(6 + 2 + 9) ⋅ 8 = 17 ⋅ 8 = 136
6 ⋅ 8 + 2 ⋅ 8 + 9 ⋅ 8 = 48 + 16 + 72 = 136