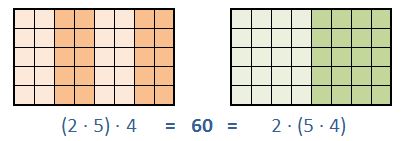As–so–z-iativgesetz → "Anders soll’s zusammen!"
Assoziativgesetz der Addition
Erklärung
Auf dieser Seite:
Lisa, Lena, Lotta, Lulu und Lara brauchen dringendst (!) neue Klamotten. Deshalb beschließen sie, nächsten Samstag einen Ausflug in die Stadt zum Shoppen zu machen.
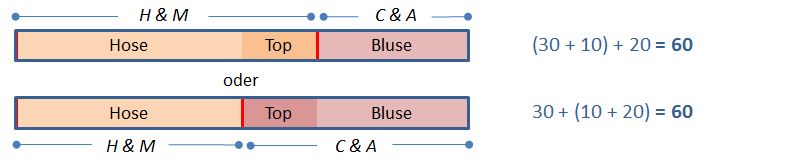
Lisa möchte eine Hose von H & M für ca. 30 Euro und die schicke Bluse von C & A für 20 Euro. Dazu soll noch ein pinkes Top für 10 Euro, egal ob von H & M oder C & A – mal schauen wer das bessere Angebot hat.
Insgesamt braucht Lisa also 60 Euro. Da passt es prima, dass sie gerade Geburtstagsgeld bekommen hat.
Es gibt also 2 Möglichkeiten, wie sich die Ausgaben auf die beiden Läden verteilen:
Mathematisch gesehen steckt dahinter das Assoziativgesetz der Addition:
Regel
Bei einer Addition von 3 Zahlen ist es egal, in welcher Reihenfolge die Summandan addiert werden, das Ergebnis &ndert sich dadurch nicht!
![]()
mehrere Summanden
Das Assoziativgesetz der Addition lässt sich aber noch verallgemeinern!
Lulu liefert hierfür ein Paradebeispiel.
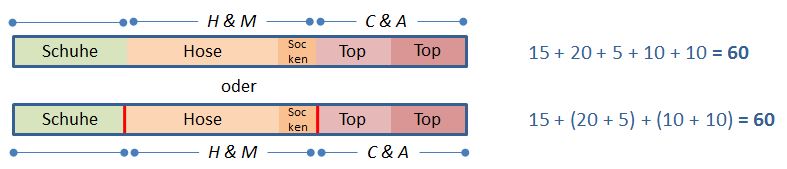
Auch sie hat 60 Euro zur Verfügung und möchte:
- ein Paar günstige Schuhe, egal von wo → 15 Euro
- eine Hose und Socken von H & M → 20 Euro + 5 Euro
- 2 Tops von C & A → 10 Euro + 10 Euro
Auch hier ist die Reihenfolge in der addiert wird egal, zum Beispiel einfach "von links nach rechts" oder zuerst die Ausgaben in den einzelnen Geschäften ausrechnen und dann die Gesamtsumme:
Assoziativgesetz der Multiplikation
Erklärung
Leider wohnen die 5 Mädels etwas abgelegen auf dem Land und benötigen deshalb noch ein Zugticket um in die Stadt zu kommen. Jeweils 4 Euro für die Hinfahrt und 4 Euro für die Rückfahrt.
Die Gesamtkosten pro Teilnehmerin belaufen sich also auf 2 ⋅ 4 Euro – das Ganze mal 5 Teilnehmerinnen.
Man kann aber auch erst die Kosten für alle pro Fahrt berechnen, also 4 ⋅ 5 Euro – wegen Hin- und Rückfahrt "2 mal":
Mathematisch gesehen steckt dahinter das Assoziativgesetz der Multiplikation:
Regel
Bei einer Multiplikation von 3 Zahlen ist es egal, in welcher Reihenfolge die Faktoren multipliziert werden, das Ergebnis &ndert sich dadurch nicht!
![]()
mehrere Faktoren
Auch das Assoziativgesetz der Multiplikation l&sst sich verallgemeinern. Soll ein Produkt aus mehr als 3 Faktoren berechnet werden, dann ist die Reihenfolge in der sie multipliziert werden egal:
(2 ⋅ 3) ⋅ (4 ⋅ 5 ⋅ 2) 2 ⋅ (3 ⋅ 4) ⋅ (5 ⋅ 2) = 240
Wofür braucht man das Assoziativgesetz?
Durch Anwendung des Assoziativgesetzes ergeben sich manchmal Rechenvorteile!
Insbesondere durch die Verallgemeinerungen mit mehreren Summanden bzw. Faktoren kann man vorteilhaft rechnen. Dazu ein paar Beispiele:
23 + 40 + 60 =
23 + (40 + 60) =
23 + 100 =
123
43 + 156 + 44 + 223 + 77 =
43 + (156 + 44) + (223 + 77) =
43 + 200 + 300 =
43 + (200 + 300) =
43 + 500 =
543
——————–
63 ⋅ 5 ⋅ 20 =
63 ⋅ (5 ⋅ 20) =
63 ⋅ 100 =
6300
8 ⋅ 125 ⋅ 2 ⋅ 5 ⋅ 13 =
(8 ⋅ 125) ⋅ (2 ⋅ 5) ⋅ 13 =
1000 ⋅ 10 ⋅ 13 =
(1000 ⋅ 10) ⋅ 13 =
10000 ⋅ 13 =
10000 ⋅ 13 =
130000
Gilt das Assoziativgesetz für alle Rechenarten?
Wie gezeigt, gilt das Assoziativgesetz für plus und mal, also Addition und Multiplikation. Das war es dann aber auch schon…
Für minus und geteilt (Subtraktion und Division) gilt das Assoziativgesetz nicht!
Subtraktion
(100 – 50) – 20 = 50 – 20 = 30
100 – (50 – 20) = 100 – 30 = 70
→ das Assoziativgesetz gilt nicht fĂĽr die Subtraktion!
Division
(100 : 10) : 5 = 10 : 5 = 2
100 : (10 : 5) = 100 : 2 = 50
→ das Assoziativgesetz gilt nicht fĂĽr die Division!
Assoziativgesetz Eselsbrücke
Die Deutsche Bezeichnung für das Assoziativgesetz lautet Verbindungsgesetz oder Verknüpfungsgesetz.
Über den Begriff Verbindungsgesetz ist es natürlich einfach auf die Regel zu kommen, denn man kann die Summanden bzw. Faktoren beliebig durch Klammersetzung verbinden bzw. verknĂĽpfen. Deshalb wird es anschaulich auch manchmal als Klammergesetz bezeichnet.
Doch wie soll man sich nun den Begriff Assoziativgesetz merken?
Wenn Du Latein kannst, ist es einfach:
associare (lat.) bedeutet verbinden, verknüpfen, vereinigen, vernetzen.
Manchmal wird das Wort auch im allgemeinen Sprachgebrauch verwendet, wenn man zum Beispiel sagt: "Mit Spanien assoziiere ich Sonne und Strand" (= "Mit Spanien verbinde ich Sonne und Strand")
Leider können heute nur noch die wenigsten Latein – also muss eine Eselsbrücke her!
As–so–z-iativgesetz → "Anders soll’s zusammen!"