Voraussetzungen
Längen umrechnen – warum und wie?
Auf dieser Seite:
Auf der EinfĂĽhrungsseite ĂĽber LängenmaĂźe wurde schon darauf hingewiesen, dass man LängenmaĂźe in andere MaĂźeinheiten umrechnen kann – ein beliebtes Thema in Klasse 5 🙂
Als Einführungsbeispiel ging es dort um den größten und den kleinsten Menschen: Robert Wadlow, der mit 2,72 m ungefähr die 5-fache Körpergröße gegenüber Chandra Bahadur Dangi mit 54,6 cm erreichen konnte.
Wie kommt man nun darauf, dass er 5 Mal so groĂź war?
Zunächst sind beide Größen in unterschiedlichen Einheiten angegeben, Meter gegenüber Zentimeter. Richtig vergleichen können wir sie aber erst, wenn beide Größen in der gleichen Einheit gegeben sind! Deshalb müssen wir sie umrechnen.
Um rechnen mit Kommazahlen zu vermeiden nehmen wir einfach Millimeter mm als Ziel-MaĂźeinheit.
- 2,72 m sind 2720 mm
- 54,6 cm sind 546 mm
- → 5 ⋅ 546 mm = 2730 mm
- → nicht ganz exakt die Größe von Robert Wadlow, aber es kommt ganz nah dran! Soo kleinlich wollen wir ja auch nicht sein
Wie man auf diese Umrechnungen kommt, erfährst Du auf dieser Seite. Es gibt dafür 2 Vorgehensweisen:
- etwas aufwändig, aber dafür sehr anschaulich und sicher: mit Hilfe einer Stellenwerttafel
- direktes Umrechnen durch Multiplikation bzw. Division
Längen umrechnen mit Stellenwerttafel
Um Längen mit Hilfe einer Stellenwerttafel in eine andere Maßeinheit umzurechnen, gehe so vor:
- Bestimme die Maßeinheit der gegebenen Länge und suche diese Spalte in der Stellenwerttafel
- Trage die Länge so ein, dass die Einerstelle der Maßzahl in dieser Spalte steht
- Suche die Spalte zur Ziel-MaĂźeinheit in der Stellenwerttafel, fĂĽlle ggf. mit Nullen auf
- Die markierte Spalte und die belegten Spalten links davon bilden die Zahl vor dem Komma – die Spalten rechts der markierten Spalte bilden die Stellen nach dem Komma
Auf der Seite LängenmaĂźe – Stellenwerttafel hast Du gelernt, LängenmaĂźe in eine Stellenwerttafel einzutragen und auch von dort auszulesen. Falls Du mit den folgenden Beispielen Schwierigkeiten hast, lies dort bitte noch einmal nach.
Denke daran, dass sich beim Auslesen immer zuerst die Frage stellt, auf welche Ziel-MaĂźeinheit man sich bezieht.
So einfach ist es, Längen mit Hilfe einer Stellenwerttafel umzurechnen!
Beispiel: 473,2 dm umrechnen
Trage 473,2 dm so ein, dass die Einerstelle (erste Zahl links vom Komma → 3) in der Spalte dm steht:

A) Umrechnung in Meter (m)
Suche die Spalte Meter und „setze dort das Komma“:

→ Ergebnis: 47,32 m
B) Umrechnung in Kilometer (km)
Suche die Spalte Kilometer, fĂĽlle mit Nullen auf und „setze dort das Komma“:

→ Ergebnis: 0,04732 km
Beispiel: 6,1003 km umrechnen
Trage 6,1003 km in die Stellenwerttafel ein:

A) Umrechnung in Dezimeter (dm)
Suche die Spalte Dezimeter und lies die Länge ab – Nachkommastellen gibt es in diesem Fall nicht:

→ Ergebnis: 61003 dm
B) Umrechnung in Millimeter (mm)
Suche die Spalte Millimeter, fülle mit Nullen auf und lies die Länge ab:

→ Ergebnis: 6.100.300 mm
Längen umrechnen durch Berechnung
Der schnellere Weg ist es, Längen direkt umzurechnen. Die Umrechnungszahlen sind:
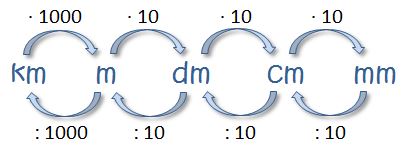
MaĂźzahl ist eine Ganze Zahl
Bei der Umrechnung von Meter in Dezimeter musst Du also zum Beispiel die MaĂźzahl mit 10 multiplizieren, in umgekehrter Richtung durch 10 dividieren.
Liegen die MaĂźeinheiten nicht direkt nebeneinander, kannst Du:
- mehrere SprĂĽnge machen – z.B. erst von Meter in Dezimeter und anschlieĂźend in Zentimeter umrechnen
- zu einem groĂźen Sprung zusammenfassen – z.B. direkt von Meter in Zentimeter durch Multiplikation mit 10 ⋅ 10 = 100
Multipliziere eine Ganze Zahl mit 10, indem Du „0 anhängst“.
Multipliziere eine Ganze Zahl mit 100, indem Du „00 anhängst“.
Multipliziere eine Ganze Zahl mit 1000, indem Du „000 anhängst“.
usw.
Eine Ganze Zahl kannst Du durch 10 teilen, wenn die letzte Stelle 0 ist. Diese „fällt dann einfach weg“.
Eine Ganze Zahl kannst Du durch 100 teilen, wenn die letzten Stellen 00 ist. Diese „fallen dann einfach weg“.
Eine Ganze Zahl kannst Du durch 1000 teilen, wenn die letzten Stellen 000 ist. Diese „fallen dann einfach weg“.
usw.
Beispiele:
A) 78 km in m:
78 km = 78 ⋅ 1000 m = 78.000 m
→ 3 Nullen wurden angehängt
B) 23 m in cm:
23 m = 23 ⋅ 10 dm = 230 dm = 230 ⋅ 10 cm = 2300 cm oder
23 m = 23 ⋅ 10 ⋅ 10 cm = 23 ⋅ 100 cm = 2300 cm
→ 2 Nullen wurden angehängt
C) 3670 mm in cm:
3670 mm = (3670 : 10) cm = 367 cm
→ 1 Null wurden gestrichen
D) 430.000 dm in km:
430.000 dm = (430.000 : 10) m = 43.000 m = (43.000 : 1000) km = 43 km oder
430.000 dm = [430.000 : (10 ⋅ 1000)] km = [430.000 : 10.000] km = 43 km
→ 4 Nullen wurden gestrichen
Bei der Umrechnung in kleinere Einheiten wird die Maßzahl größer.
Bei der Umrechnung in größere Einheiten wird die Maßzahl kleiner.
MaĂźzahl ist eine Kommazahl
Multipliziere eine Kommazahl mit 10, indem Du „das Komma um 1 Stelle nach rechts verschiebst“.
Multipliziere eine Kommazahl mit 100, indem Du „das Komma um 2 Stellen nach rechts verschiebst“.
Multipliziere eine Kommazahl mit 1000, indem Du „das Komma um 3 Stellen nach rechts verschiebst“.
usw.
Dabei fällt ab der Einerstelle das Komma komplett weg – hänge statt verschieben dann jeweils eine 0 an.
Teile eine Kommazahl durch 10, indem Du „das Komma um 1 Stelle nach links verschiebst“.
Teile eine Kommazahl durch 100, indem Du „das Komma um 2 Stellen nach links verschiebst“.
Teile eine Kommazahl durch 1000, indem Du „das Komma um 3 Stellen nach links verschiebst“.
usw.
Gibt es zu wenige Stellen um das Komma nach links zu schieben, dann „hänge vor der Zahl Nullen an“.
Beispiele:
A) 53,954 km in m:
53,954 km = 53,954 ⋅ 1000 m = 53954 m
→ Komma um 3 Stellen nach rechts verschoben
→ hinter der Einerstelle fällt es weg
B) 24,841 m in cm:
24,841 m = 24,841 ⋅ 10 dm = 248,41 dm = 248,41 ⋅ 10 cm = 2484,1 cm oder
24,841 m = 24,841 ⋅ 10 ⋅ 10 cm = 24,841 ⋅ 100 cm = 2484,1 cm
→ Komma um 2 Stellen nach rechts verschoben
C) 83,2 dm in mm:
83,2 dm = 83,2 ⋅ 10 cm = 832 cm = 832 ⋅ 10 mm = 8320 mm oder
83,2 dm = 83,2 ⋅ 10 ⋅ 10 mm = 83,2 ⋅ 100 mm = 8320 mm
→ Komma um 2 Stellen nach rechts verschoben
→ da es nur eine Nachkommastelle gibt, fällt es nach der ersten Verschiebung weg
→ statt der zweiten Verschiebung wird eine Null angehängt
D) 25,2 cm in dm:
25,2 cm = (25,2 : 10) dm = 2,52 dm
→ Komma um 1 Stelle nach links verschoben
E) 13,12 dm in km:
13,12 dm = (13,12 : 10) m = 1,312 m = (1,312 : 1000) km = 0,001312 km oder
13,12 dm = [13,12 : (10 ⋅ 1000)] km = [13,12 : 10.000] km = 0,001312 km
→ Komma um 4 Stellen nach links verschoben
→ da es nur zwei Vorkommastellen gibt, mĂĽssen „vorne zwei Nullen angehängt werden“
