Komm–u–ta-tivgesetz → "Komm und tausche!"
Kommutativgesetz der Addition
Erklärung
"Jetzt ist mal Schluss am Computer! Such Dir aus, was du zuerst machen möchtest: Hausaufgaben oder Zimmer aufräumen?", versucht Mama ihren Max zu motivieren.
Auf dieser Seite:
"Eigentlich will ich ja noch weiter zocken – aber wenn man ganz ehrlich ist hat sie ja irgendwie Recht…", denkt sich Max. "Für die Hausaufgaben werde ich so 45 Minuten brauchen – Zimmer aufräumen schaffe ich locker in 15 Minuten.", setzt er seinen Gedankengang fort. Doch wie Max es dreht und wendet: "Egal mit was ich anfange: Die nächste Stunde bin ich wohl beschäftigt."
Das hat Max ganz richtig erkannt: Die Reihenfolge spielt für die Gesamtzeit keine Rolle. Es ist jetzt 17:00 Uhr – um 18:00 Uhr wird Max fertig sein. So oder so…
Mathematisch gesehen steckt dahinter das Kommutativgesetz der Addition:
Regel
Bei der Addition dürfen die Summandan vertauscht werden, das Ergebnis ändert sich dadurch nicht!
![]()
mehrere Summanden
Das Kommutativgesetz der Addition lässt sich aber noch verallgemeinern! Angenommen, die Hausaufgaben setzen sich zusammen aus 20 Minuten Mathe, 15 Minuten Englisch und 10 Minuten Biologie (= 45 Minuten).
Klar, auch hier ist die Reihenfolge egal: Max braucht insgesamt 45 Minuten für seine Hausaufgaben! Max könnte auch seine Hausaufgaben unterbechen und zwischendurch aufräumen – die Gesamtzeit ändert sich nicht.
Es gibt natürlich noch andere Möglichkeiten, aber zum Beispiel:
Kommutativgesetz der Multiplikation
Erklärung
Für die Englisch-Hausaufgaben muss Max 15 Vokabeln abschreiben und lernen. Da er sich nicht alles auf einmal merken kann, teilt er die Vokabeln in Blöcke ein und macht immer erst weiter, wenn er den Block einigermaßen beherrscht.
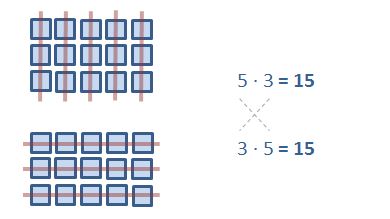
Für die 15 Vokabeln gibt es zwei mögliche Aufteilungen – 5 Blöcke mit jeweils 3 Vokabeln oder 3 Blöcke mit jeweils 5 Vokabeln:
Mathematisch gesehen steckt dahinter das Kommutativgesetz der Multiplikation:
Regel
Bei der Multiplikation dürfen die Faktoren vertauscht werden, das Ergebnis ändert sich dadurch nicht!
![]()
mehrere Faktoren
Auch das Kommutativgesetz der Multiplikation lässt sich verallgemeinern. Soll ein Produkt aus mehr als 2 Faktoren berechnet werden, dann dürfen diese beliebig vertauscht werden.
2 ⋅ 3 ⋅ 4 ⋅ 5 =
3 ⋅ 5 ⋅ 2 ⋅ 4 =
120
Wofür braucht man das Kommutativgesetz?
Insbesondere durch die Verallgemeinerungen mit mehreren Summanden bzw. Faktoren kann man vorteilhaft rechnen!
Dazu ein paar Beispiele:
80 + 40 + 20 =
80 + 20 + 40 =
100 + 40 =
140
156 + 223 + 56 + 44 + 77 =
156 + 44 + 223 + 77 + 56 =
200 + 223 + 77 + 56 =
423 + 77 + 56 =
500 + 56 =
556
——————–
25 ⋅ 7 ⋅ 4 =
4 ⋅ 25 ⋅ 7 =
100 ⋅ 7 =
700
125 ⋅ 13 ⋅ 2 ⋅ 8 ⋅ 5 =
8 ⋅ 125 ⋅ 5 ⋅ 2 ⋅ 13 =
1000 ⋅ 5 ⋅ 2 ⋅ 13 =
5000 ⋅ 2 ⋅ 13 =
10000 ⋅ 13 =
130000
Durch Anwendung des Kommutativgesetzes ergeben sich manchmal Rechenvorteile!
Gilt das Kommutativgesetz für alle Rechenarten?
Wie gezeigt, gilt das Kommutativgesetz für plus und mal, also Addition und Multiplikation. Das war es dann aber auch schon…
Subtraktion
Du hast 10 Euro und kaufst für 3 Euro ein Eis → rechne "10 – 3"
→ es bleiben 7 Euro
Du hast 3 Euro und möchtest für 10 Euro ins Kino gehen → rechne "3 – 10"
→ das Geld reicht nicht!
Division
4 Euro werden unter 2 Geschwistern aufgeteilt → rechne "4 Euro : 2"
→ jeder bekommt 2 Euro
2 Euro werden unter 4 Geschwistern aufgeteilt → rechne "2 Euro : 4"
→ jeder bekommt 50 Cent
Für minus und geteilt (Subtraktion und Division) gilt das Kommutativgesetz nicht!
Kommutativgesetz Eselsbrücke
Die Deutsche Bezeichnung für das Kommutativgesetz lautet Vertauschungsgesetz.
Über den Begriff Vertauschungsgesetz ist es natürlich einfach auf die Regel zu kommen, denn die Summanden bzw. Faktoren sind links und rechts vom Gleichheitszeichen jeweils einfach getauscht.
Doch wie soll man sich nun den Begriff Kommutativgesetz merken?
Wenn Du Latein kannst, ist es einfach: commutare (lat.) bedeutet tauschen.
Leider können heute nur noch die wenigsten Latein – also muss eine Eselsbrücke her!
Komm–u–ta-tivgesetz → "Komm und tausche!"