direkte proportionale Zuordnung – Beispiel
Auf dieser Seite:
Die Klasse 7b hat abgestimmt! Es ging um die Frage, wohin der Ausflug am nächsten Wandertag gehen solle?
Von den Schülern wurde der Vorschlag „Phantasialand“ gemacht. Der Gegenvorschlag von Lehrer Oberschlau sah einen Besuch des kürzlich neueröffneten „Museum für prähistorische Entwicklungen der Kunstgeschichte im Neandertal“ vor.
Mit dem knappen Ergebnis von 24 zu 1 Stimmen (Herr Oberschlau stimmte mit ab) wurde entschieden, verschiedene physikalische Gesetzmäßigkeiten – wie zum Beispiel den freien Fall – im Phantasialand live zu erleben.
Soweit so gut. Die nächste Frage ist, wie die Klasse 7b ins Phantasialand kommen soll? Bahn oder Bus? Da die Fahrzeit für beides ungefähr gleichlang ist, soll es möglichst günstig sein. Herr Oberschlau darf als Begleitperson umsonst fahren.
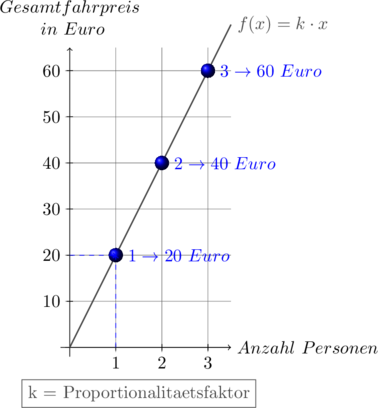
Eine Fahrkarte für die Bahn kostet pro Person 20 Euro.
direkt proportionale Zuordnung
→ „je mehr, desto mehr“
Würde ein Schüler alleine fahren, betrügen die gesamten Fahrtkosten mit der Bahn 20 Euro. Fährt er zusammen mit seinem Freund (→ doppelt soviele Personen), verdoppelt sich auch der Gesamtpreis. Fährt die ganze Klasse (→ 24 mal so viele Personen), wird auch der 24-fache Gesamtpreis fällig. Je mehr Personen eine Fahrkarte kaufen, desto höher ist der gesamte Fahrpreis.
Entscheidend für den Zusammenhang zwischen Anzahl der Personen und den gesamten Fahrtkosten ist aber Folgendes:
doppelte Personenzahl → doppelter Preis
dreifache Personenzahl → dreifacher Preis
…
Definition: direkt proportionale Zuordnung
Zwischen zwei Größen x und y besteht eine direkt proportionale Zuordnung, wenn dem Doppelten (3-fachen, …, n-fachen) der einen Größe das Doppelte (3-fache, …, n-fache) der anderen Größe zugeordnet ist.
Man sagt dann x ist proportional zu y und schreibt x ~ y.
Diese Definition gilt natürlich auch für Bruchteile, also zum Beispiel die Hälfte, ein Drittel, zwei Drittel, usw.
Definition: Proportionalitätsfaktor
Die Größen einer proportionalen Zuordnung sind verhältnisgleich, das heißt, die eine Größe geht aus der anderen durch Multiplikation mit einem immer gleichen Faktor hervor.
Diesen Faktor nennt man Proportionalitätsfaktor (k) oder Proportionalitätskonstante. Man berechnet ihn, indem man die zugeordnete Größe durch die erste Größe dividiert:
Mathematisch ausgedrückt:
Wenn x → y und x ~ y, dann ![]() .
.
In unserem Beispiel erhält man jeweils den Gesamtpreis, indem man die Anzahl der Fahrkarten mit dem festen Wert 20 Euro multipliziert. Der Proportionalitätsfaktor beträgt also in diesem Fall k = 20 Euro.
Proportionalität – häufige Fehler
Es kommt oft vor, dass zwei Größen in einer Beziehung nach dem Motto „je mehr, desto mehr“ stehen.
Aber Achtung: Das bedeutet nicht automatisch, dass die beiden Größen auch proportional zueinander sind!
Beispiele:
- Ein Baby wächst in seinem ersten Lebensjahr ca. 30 cm. Ist es doppelt so alt, ist es aber nicht auch doppelt so groß.
- …
- Je größer ein Päckchen ist, desto mehr Porto kostet es. Jodoch ist das Porto nicht doppelt so hoch, wenn das Päckchen doppelt so groß ist
direkt proportionale Zuordnung
– Darstellung als Graph
Die jeweils zugeordneten Größenpaare lassen sich in einem Koordinatensystem als Punkte eintragen.
Verbindet man diese Punkte, dann liegen sie alle auf einer Geraden durch den Ursprung:
Weiter geht’s mit: Antiproportionale Zuordnung

