antiproportionale Zuordnung – Beispiel
Auf dieser Seite:
Die Klasse 7b hat in einer spannenden Abstimmung beschlossen, dass der Ausflug am nächsten Wandertag ins Phantasialand gehen soll.
Die Frage ist noch, ob es günstiger ist, mit der Bahn oder mit dem Bus dorthin zu fahren? Eine Fahrkarte für die Bahn kostet pro Person 20 Euro. Für den Bus liegt ein Angebot über insgesamt 600 Euro vor.
Das ist nun schnell ausgerechnet! Teilt man die Gesamtrechnung über 600 Euro auf die 24 Schüler der Klasse 7b auf, dann ergibt das pro Kopf 600 Euro : 24 = 25 Euro – teurer als die Fahrt mit der Bahn.
Herr Oberschlau hat aber eine Idee. Im Bus ist ja noch jede Menge Platz und Herr Sonntag, der Klassenlehrer der 7d ist einer seiner besten Freunde. Wie wäre es, wenn sie einfach zusammenfahren?
In der Klasse 7d sind ebenfalls 24 Schüler. Wie hoch sind die Kosten für den Bus pro Schüler, wenn die 7b mit der 7d zusammen ins Phantasialand fährt?
antiproportionale Zuordnung
→ „je mehr, desto weniger“
Dem Busunternehmen ist es egal, wie voll der Bus besetzt ist. Der Fahrpreis für den ganzen Bus ist auf jeden Fall fest. Je mehr Personen mitfahren, desto weniger ist pro Mitfahrer zu bezahlen.
Entscheidend für den Zusammenhang zwischen Anzahl der Personen und Fahrtkosten pro Kopf ist aber Folgendes:
doppelte Personenzahl → der Fahrpreis pro Kopf beträgt die Hälfte
dreifache Personenzahl → der Fahrpreis pro Kopf beträgt ein Drittel
…
Definition: antiproportionale Zuordnung
Zwischen zwei Größen x und y besteht eine antiproportionale Zuordnung, wenn dem Doppelten (3-fachen, …, n-fachen) der einen Größe die Hälfte (ein Drittel, …, ein n-tel) der anderen Größe zugeordnet ist.
Man sagt dann x ist antiproportional zu y oder auch x ist umgekehrt proportional zu y oder auch x ist indirekt proportional zu y.
Für x ist antiproportional zu y schreibt man kurz x ~ ![]() .
.
Diese Definition gilt natürlich auch für Bruchteile, also zum Beispiel wird der Hälfte das Doppelte zugeordnet, einem Drittel das Dreifache, usw.
Definition: Antiproportionalitätskonstante
Für Größen einer antiproportionalen Zuordnung gilt, dass ihr Produkt für alle Wertepaare konstant ist.
Dieses Produkt nennt man Antiproportionalitätskonstante (k) (oder manchmal auch Antiproportionalitätsfaktor). Man berechnet k, indem man zwei zugeordnete Größen miteinander multipliziert.
Mathematisch ausgedrückt:
Wenn x → y und x ~ ![]() , dann
, dann ![]() .
.
In unserem Beispiel ergibt sich, dass durch die Teilnahme der Klasse 7d (→ doppelt so viele Schüler) der Fahrpreis pro Kopf von 25 Euro auf 12,50 Euro gesenkt werden kann (→ halber Preis). Die Antiproportionalitätskonstante war in diesem Fall mit k = 600 Euro bereits gegeben.
antiproportionale Zuordnung –
Darstellung als Graph
Die jeweils zugeordneten Größenpaare lassen sich in einem Koordinatensystem als Punkte eintragen.
Verbindet man diese Punkte, dann liegen sie alle auf einer Hyperbel:
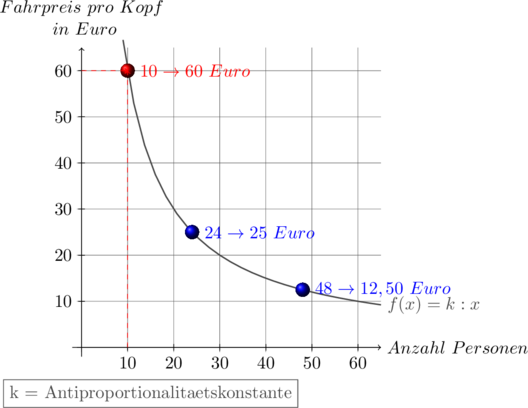
Man sieht in der Graphik: Würden nur 10 Schüler mitfahren, dann erhöhte sich der Preis pro Kopf auf 60,00 Euro! In diesem Fall ginge es dann wohl doch ins „Museum für prähistorische Entwicklungen der Kunstgeschichte im Neandertal“ 😉

